03 单向链表

单向链表

单向链表是一种线性数据结构，其每个节点包含数据和指向下一节点的指针。适用于频繁插入和删除操作的场景。

简介

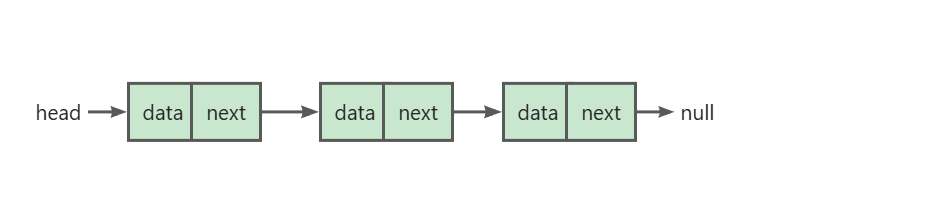
链表（linked list）的组成单位是节点（node）对象。每个节点都包含两项数据：节点的“值”和指向下一节点的“引用”。

• 链表的首个节点被称为“头节点”，最后一个节点被称为“尾节点”

• 单向链表的最后一个节点指向“空”，表示链表的结束；在 Java、C++ 和 Python 中分别记为 null、nullptr和 None

• 在 C、C++、Go、Rust 等支持指针的语言中，“引用”应替换为“指针”

• 引用记录了下一节点的内存地址，通过它可以从当前节点访问到下一节点

核心特性

1. 动态大小：链表可以动态增长和缩小，无需预先定义大小

2. 非连续性存储：节点在内存中分散存储，通过指针相连

3. 单向性：每个节点只知道下一节点在哪里，不知道上一节点

4. 顺序访问：必须从头节点开始，沿着指针逐个访问节点

5. 无索引访问：不能像数组那样通过索引直接访问元素

基本操作

时间复杂度分析

基础实现

// 定义节点类
class Node {
    int data;       // 数据域
    Node next;      // 指针域，指向下一个节点
    
    // 构造函数
    public Node(int data) {
        this.data = data;
        this.next = null;
    }
}

// 单向链表类
class SinglyLinkedList {
    private Node head;  // 头节点
    
    // 构造函数，创建一个空链表
    public SinglyLinkedList() {
        this.head = null;
    }
    
    // 判断链表是否为空
    public boolean isEmpty() {
        return head == null;
    }
    
    // 在链表头部插入节点
    public void insertAtHead(int data) {
        Node newNode = new Node(data);
        if (isEmpty()) {
            head = newNode;
        } else {
            newNode.next = head;
            head = newNode;
        }
    }
    
    // 在链表尾部插入节点
    public void insertAtTail(int data) {
        Node newNode = new Node(data);
        if (isEmpty()) {
            head = newNode;
            return;
        }
        
        Node current = head;
        // 找到最后一个节点
        while (current.next != null) {
            current = current.next;
        }
        current.next = newNode;
    }
    
    // 在指定位置插入节点
    public void insertAtPosition(int data, int position) {
        // 位置无效
        if (position < 0) {
            System.out.println("位置无效");
            return;
        }
        
        // 插入位置为0，相当于在头部插入
        if (position == 0) {
            insertAtHead(data);
            return;
        }
        
        Node newNode = new Node(data);
        Node current = head;
        Node previous = null;
        int count = 0;
        
        // 找到要插入位置的前一个节点
        while (current != null && count < position) {
            previous = current;
            current = current.next;
            count++;
        }
        
        // 如果position超出链表长度，则插入到尾部
        previous.next = newNode;
        newNode.next = current;
    }
    
    // 删除第一个值为data的节点
    public void delete(int data) {
        // 链表为空
        if (isEmpty()) {
            System.out.println("链表为空，无法删除");
            return;
        }
        
        // 删除的是头节点
        if (head.data == data) {
            head = head.next;
            return;
        }
        
        // 删除的不是头节点
        Node current = head;
        Node previous = null;
        
        // 查找要删除的节点
        while (current != null && current.data != data) {
            previous = current;
            current = current.next;
        }
        
        // 如果找到了要删除的节点
        if (current != null) {
            previous.next = current.next;
        } else {
            System.out.println("未找到要删除的元素");
        }
    }
    
    // 查找节点
    public boolean search(int data) {
        if (isEmpty()) {
            return false;
        }
        
        Node current = head;
        while (current != null) {
            if (current.data == data) {
                return true;
            }
            current = current.next;
        }
        return false;
    }
    
    // 打印链表
    public void display() {
        if (isEmpty()) {
            System.out.println("链表为空");
            return;
        }
        
        Node current = head;
        while (current != null) {
            System.out.print(current.data + " -> ");
            current = current.next;
        }
        System.out.println("null");
    }
    
    // 获取链表长度
    public int size() {
        int count = 0;
        Node current = head;
        while (current != null) {
            count++;
            current = current.next;
        }
        return count;
    }
}

// 使用示例
public class LinkedListDemo {
    public static void main(String[] args) {
        SinglyLinkedList list = new SinglyLinkedList();
        
        list.insertAtTail(10);
        list.insertAtTail(20);
        list.insertAtTail(30);
        list.insertAtHead(5);
        list.display();  // 输出: 5 -> 10 -> 20 -> 30 -> null
        
        list.insertAtPosition(15, 2);
        list.display();  // 输出: 5 -> 10 -> 15 -> 20 -> 30 -> null
        
        list.delete(15);
        list.display();  // 输出: 5 -> 10 -> 20 -> 30 -> null
        
        System.out.println("查找结果: " + list.search(20));  // 输出: 查找结果: true
        System.out.println("链表长度: " + list.size());      // 输出: 链表长度: 4
    }
}

优缺点

优点

• 动态大小：链表可以根据需要动态分配内存，不需要预先定义大小

• 插入和删除高效：在已知位置插入或删除节点的时间复杂度为 O(1)

• 内存利用灵活：不需要连续的内存空间，可以充分利用可用内存

• 实现简单：基本操作实现相对简单直观

缺点

• 随机访问低效：无法通过数组那样通过索引直接访问元素，必须从头开始遍历

• 额外内存开销：每个节点除了存储数据外，还需要存储指针，增加了内存消耗

• 缓存不友好：由于内存不连续，不能有效利用 CPU 缓存，可能导致性能下降

• 反向遍历困难：单向链表不支持反向遍历

应用场景

• 作为其他数据结构的基础：

• 栈与队列

• 哈希表

• 图

• 历史记录

• 撤销功能：编辑器撤销操作

扩展

双向链表

循环链表（环形链表）

热门题目

• 206. 反转链表

• 21. 合并两个有序链表

• 141. 环形链表

• 19. 删除链表的倒数第 N 个结点

• 160. 相交链表

206. 反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例：

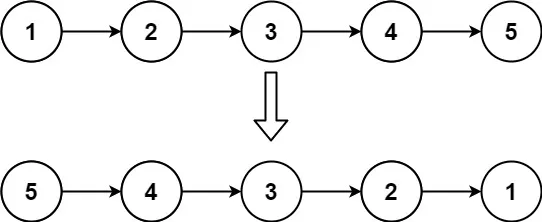
输入：head = [1,2,3,4,5]

输出：[5,4,3,2,1]

题解：

双指针（迭代）

遍历链表时，修改各节点的引用指向

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode pre = null;
        ListNode cur = head;

        while (cur != null) {
            ListNode nextTemp = cur.next;  // 暂存下一节点
            cur.next = pre;                // 反转当前节点指针
            pre = cur;                     // 移动 pre 指针
            cur = nextTemp;                // 移动当前节点 cur 指针
        }

        return pre;                        // 最终 pre 指向新链表的头节点
    }
}

###